Abstract

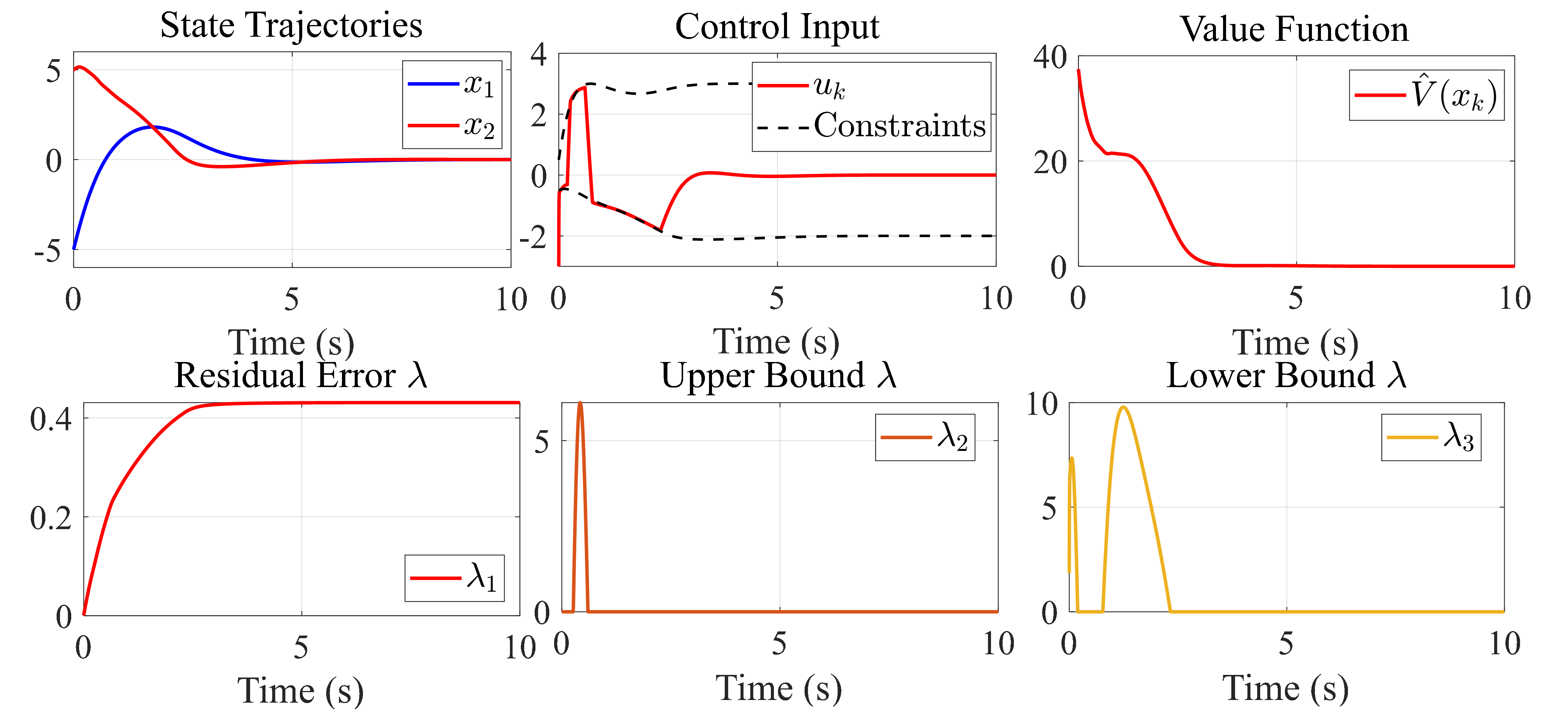
This paper proposes an online reinforcement learning algorithm that directly solves the Bellman optimality equation by casting it as a constrained optimization problem. Unlike policy or value iteration, which incrementally approximate the Bellman (optimality) equation, the method treats the value function and control policy as joint decision variables and solves them simultaneously. The formulation also permits systematic incorporation of additional constraints, such as input or safety limits. Direct solution of the Bellman optimality equation enables coordinated value–policy updates that stabilize online adaptation. Explicit constraint handling ensures per-step feasibility in online settings. The problem is addressed using a Lagrangian-based primal–dual approach, resulting in online update laws that drive the Bellman error toward zero while satisfying all constraints. The effectiveness of the method is demonstrated on a constrained nonlinear optimal control task.

Additional Comments