Abstract

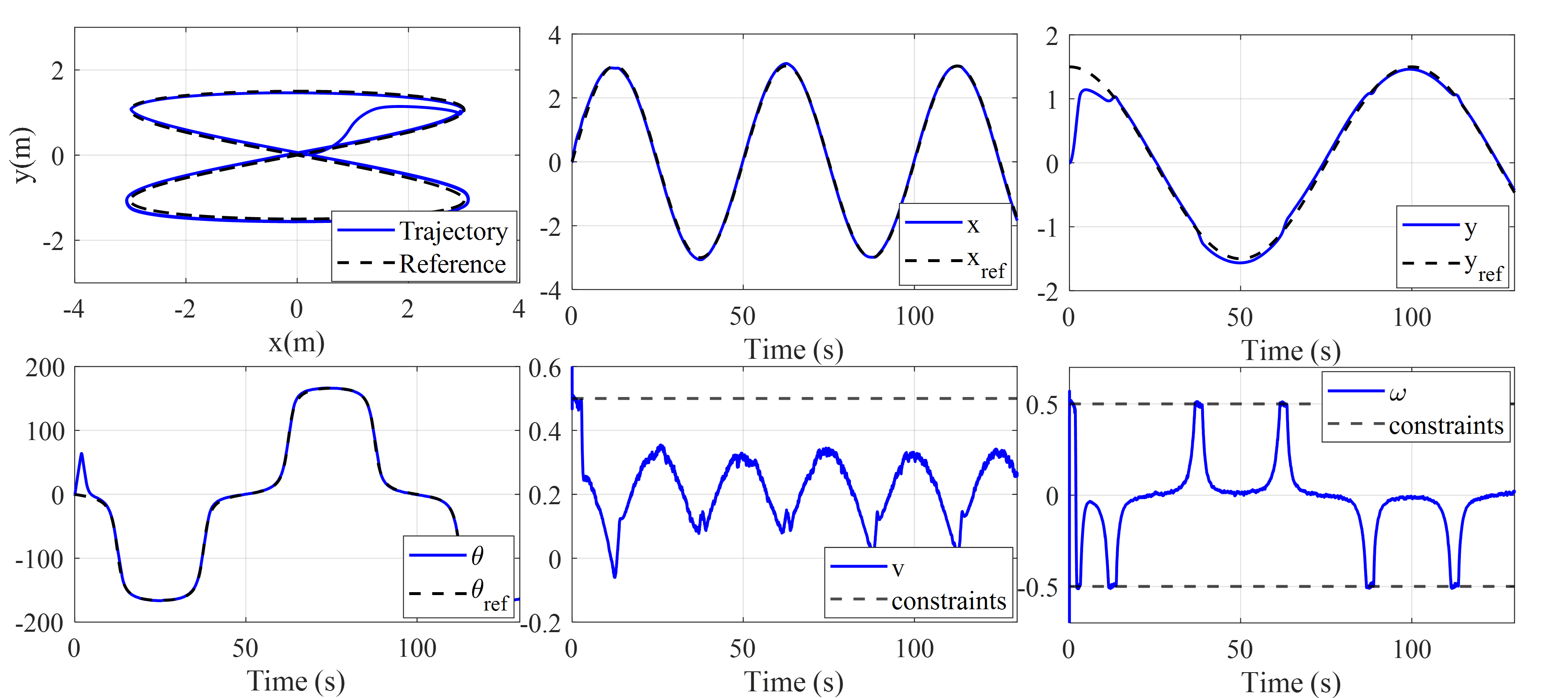
This paper presents a constrained online reinforcement learning framework for the optimal tracking control of constrained nonlinear systems. While reinforcement learning provides powerful tools for optimal control, conventional implementations typically rely on unconstrained minimization strategies. Since this approach does not restrict the policy search space within the feasible region, it often drives the control policy toward unbounded actions, exacerbating the instability inherent in nonlinear function approximation. To address these issues, the proposed method reformulates the Bellman optimality equation as a constrained optimization problem where the control policy and value function are treated as joint decision variables. Crucially, this formulation allows for the explicit incorporation of system constraints directly into the learning process. A Lagrangian-based primal-dual scheme is then employed to find a Karush-Kuhn-Tucker solution, ensuring strict constraint satisfaction. Experimental validation on a differential-wheeled mobile robot demonstrates that the algorithm strictly enforces hard constraints during complex maneuvers while maintaining stable convergence of the value function.

Additional Comments